Кинематическое исследование пространственных планетарных механизмов методом планов угловых скоростей.

Рассмотрим этот метод исследования на примере планетарного механизма конического дифференциала заднего моста автомобиля. На рис. 15.8 изображена схема механизма и планы угловых скоростей.

Планы угловых скоростей строятся в соответствии с векторными уравнениями:

w2=w1+w21; w4=w3+w43

w3=w2+w32 ; w5=w3+w53

Вектора относительных угловых скоростей направлены по осям мгновенного относительного вращения:

w 21 - по линии контакта начальных конусов звеньев 2 и 1 ;
w 32 - по оси шарнира С ;
w 43 4 и 3 ;
w 53 - по линии контакта начальных конусов звеньев 5 и 3 .

Вектора абсолютных угловых скоростей направлены по осям кинематических пар, которые образуют звенья со стойкой:

w 2 - по оси пары В ;w 1 - по оси пары А ;
w 4 - по оси пары Е ; w 5 - по оси пары D .

Направление угловой скорости сателлита 3 определяется соотношением величин угловых скоростей w 2 и w 32 .

Рассмотрим три режима движения автомобиля:

• прямолинейное движение w 4 = w 5 (векторная диаграмма на рис.15.8a). В этом режиме движения корпус дифференциала 2 и полуоси 4 и 5 вращаются с одинаковыми угловыми скоростями w 4 = w 5 = w 2 , а относительная угловая скорость сателлита w 32=0 .
• поворот автомобиля направо w 4 w5 (векторная диаграмма на рис.15.8б). При повороте направо угловые скорости полуосей не равны и связаны неравенством w 4 w5 ,поэтому сателлит будет вращаться с такой угловой скоростью w 32 , которая обеспечивает постоянство угловой скорости корпуса дифференциала w 2.
• буксование левого колеса w 4 = 0 (векторная диаграмма на рис.15.8в). При буксовании левого колеса, правое колесо останавливается w 4 = 0 , а левое будет вращаться с угловой скоростью w5 = 2Ч w 2 .

Для того, чтобы в условиях низкого сцепления колес с грунтом, уменьшить опасность их пробуксовывания в дифференциалы автомобилей высокой проходимости включают элементы трения или блокировки.

Контрольные вопросы к лекции 15

1. Какой зубчатый механизм называется сложным?(стр.1)

2. Какой механизм называется планетарным? (стр.1)

3. Как определить передаточное отношение одной из схем планетарного редуктора аналитическим способом?(стр.2-4)

4. Как используются графический и аналитический способы для определения угловых скоростей звеньев планетарных зубчатых механизмов?(стр.6-9)

5. Как устанавливаются кинематические зависимости в планетарном зубчатом механизме с коническими колесами?(стр.1-11)

6. Как используется графический способ для определения угловых скоростей звеньев дифференциалов?(стр.10-11)

7. Какова цель применения метода обращения движения при кинематическом анализе планетарных механизмов?(стр.4-6)

Кинематика зубчатых механизмов

Зубчатая передача, у которой геометрическая ось хотя бы од­ного из колес подвижна, называется планетарной . Различные плане­тарные механизмы можно представить в виде трех типов передач.

1. Простые планетарные передачи, обладающие одной степенью подвижности, у которых одно из основных звеньев закреплено непо­движно (рис. 15.7, закреплено звено 3). Такие механизмы служат для последовательной передачи потока мощности.

2. Дифференциальные передачи, обладающие двумя степенями подвижности, у которых все основные звенья подвижны (рис. 15.6). Эти передачи позволяют суммировать два или несколько потоков мощнос­ти, поступающих от независимых источников, либо распределять их по независимым потребителям.

3. Замкнутые дифференциальные передачи, получаемые из дифференциальных передач путем замыкания двух основных звеньев (центрального колеса и водила) простой передачей, состоящей из колес 1, 2, 3 (рис. 15.8). Такие передачи позволяют получить большие пе­редаточные отношения при малых габаритах.

Рассмотрим механизм, изображенный на рис. 15.6. Определим число степеней подвижности, если = 4 - число звеньев,и – число кинематических пар V и IV класса.

Определенность в движении звеньев уэтого механизма будет в том случае, если будут заданы законы движения двум звеньям.

Основными звеньями механизмов с подвижными осями являются водило (Н) и соосные с ним колеса (1 и 3). В данном случае все основные звенья подвижные. Оба эти признака (W> 1 и подвижные основные звенья) определяют дифференциальный механизм .

Определим степень подвижности для механизма, изображенного на
рис. 15.7

У этого механизма колесо 3 (основное звено) неподвижно и W= 1. Оба признака определяют планетарный механизм .

Механизмы замкнутых дифференциалов имеют все основные звенья подвижными, но число степеней подвижности равно единице (W= 1). Таким об­разом, только по совокупности двух признаков механизмы с подвиж­ными осями можно отнести к тому или иному типу.

Формулы 15.5, 15.7 для определения передаточного отношения планетарных и дифференциальных механизмов использовать нельзя, так как сателлит участвует в сложном движении, состоящем из вра­щения вокруг оси O 2 и вращения вместе с водилом Н вокруг оси О н (см. рис.15.6, 15.7).

Для вывода зависимостей, связывающих угловые скорости меха­низмов, имеющих подвижные оси, воспользуемся методом обращения движения.

Допустим, что в действительном движении звенья механизма (см.рис.15.6) имеют угловые скорости . Сооб­щим всем звеньям скорость, равную угловой скорости водила, но противоположно ей направленную, т.е. . В этом случае угловые скорости звеньев будут соответственно равны:

Так как водило Н стало неподвижным (), то мы получили "обращенный механизм" с неподвижными осями. Для этого меха­низма справедлива зависимость

где –передаточное отношение "обращенного механизма, кото­рое можно определить через число зубьев колес:

В правую часть предыдущей зависимости подставим значение относительных скоростей:

(15.9)

Полученное уравнение называется формулой Виллиса для дифференциальных механизмов . Левая часть, как показано выше, может быть выражена через число зубьев колес. Определенность в решении правой части будет иметь место, когда будут известны скорости двух ведущих звеньев. Установим, какой вид примет формула Вилли­са для планетарного механизма, изображенного на рис. 15.7. У этого механизма колесо 3 жестко соединено со стойкой (заторможено), т.е. .

Таким образом, имеем

Откуда (15.10)

Полученную зависимость называют формулой Виллиса для плане­тарных механизмов, а передаточное отношение – планетарным передаточным отношением .

Как и для дифференциальных механизмов, определяется че­рез число зубьев колес.

В общем случае:

где – передаточное отношение от звена К к звену l (l – соответствует неподвижному центральному колесу).

Достоинством планетарных механизмов является возможность получения больших передаточных отношений при малых габаритах.

Пример 1 . Определить передаточное отношение планетар­ного механизма (рис. 15.9), если Z 1 = 100, Z 2 = 99, Z 2´ = 100, Z 3´ = 101.Это одноступенчатый планетарный редуктор. Используя формулу (15.10), запишем

Пример 2 . В зубчатой передаче, показанной на рис. 15.10, входное коническое колесо 1 в данный момент имеет угловую ско­рость = 340 с -1 и постоянное угловое ускорение = 285 с -2 , направленное по движению.

Z 1 = Z 2 = 18; Z 2´ = Z 4´ = 18; Z 3 = Z 5 = 30; Z 3´ = Z 5´ = 22; Z 4 = Z 6 = 70.

Принять средний модуль конического колеса m m = 2 мм, шири­ну колеса b= 20 мм, плотность ρ = 8000 кг/м, смещение центра масс (точки А, рис.15.11) l = 2 мм.

Определить:

1) передаточное отношение между входным и выходным звеньями и направление вращения;

2) угловую скорость и угловое ускорение выходного звена, их направление показать на схеме передачи;

3) время, в течение которого угловая скорость увеличится в 2 раза;

4) величину и направление силы инерции и момента пары сил инерции звена 1 в начале и в конце найденного в предшествующем пункте промежутка времени, сравнить силу инерции с силой тяжести и показать чертежом направления вращения, ускорения и инерцион­ных нагрузок;

5) общий коэффициент полезного действия передачи.

1. Определить передаточное отношение механизма.

Выделим из механизма ступень с неподвижными осями, состоящую

Кинематика планетарных механизмов

Краткое содержание: Многозвенные зубчатые механизмы. Кинематика рядового зубчатого механизма. Кинематика ступенчатого механизма. Формула Виллиса для планетарных механизмов. Кинематическое исследование типовых планетарных механизмов графическим и аналитическим методами.

При проектировании зубчатых механизмов многих машин и приборов (манипуляторов, станков, автомобилей, летательных аппаратов, индикаторов, тахометров, печатающих устройств ЭВМ и др.) возникает необходимость обеспечить передачу вращения с большим передаточным отношением или при значительных межосевых расстояниях. В таких случаях применяют многозвенные зубчатые механизмы либо снижающие скорость вращения выходного вала по сравнению с входным - редукторы, либо повышающие ее - мультипликаторы.

Многозвенные зубчатые механизмы могут быть как плоскими, так и пространственными. Они подразделяются на два основных вида:

зубчатые механизмы с неподвижными осями всех колес;

зубчатые механизмы, оси отдельных колес которых перемещаются относительно стойки.

К первому виду механизмов относятся рядовые (с развернутой схемой) и ступенчатые зубчатые механизмы, подвижность таких механизмов

. Ко второму виду относятся планетарные , дифференциальные

, замкнутые дифференциальные и волновые зубчатые механизмы. Большим достоинством механизмов второго вида является их компактность. Проектирование многозвенных зубчатых механизмов включает два этапа: выбор структурной схемы; определение чисел зубьев для воспроизведения заданного передаточного отношения.

Общее передаточное отношение многозвенного механизма равно произведению передаточных отношений отдельных механизмов (ступеней), последовательно включенных в его состав

Кинематика рядового зубчатого механизма

Рядовым зубчатым механизмом называется сложный зубчатый механизм с неподвижными осями колес, образованный последовательным соединением нескольких пар единичных зубчатых колес. Имея схему передачи и числа зубьев или радиусы начальных окружностей колес можно определить общее передаточное отношение такого редуктора аналитически или графически. (Для колес без смещения, которые обычно используют в редукторах , начальные окружности совпадают с делительными; для колес со смещением -

).

Рассмотрим кинематику рядового механизма составленного из трех зубчатых передач внешнего зацепления. Схема механизма изображена на рис.

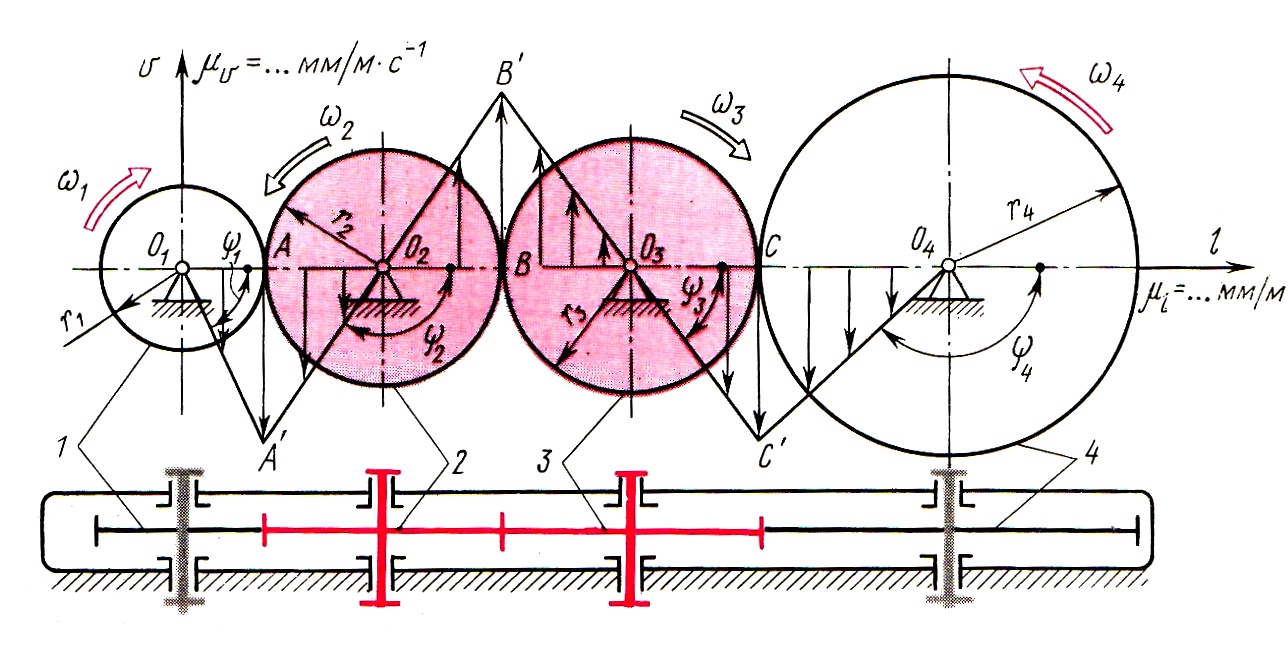
, где знак «+» соответствует внешнему зацеплению зубчатых колес, а знак «-» внутреннему.

Таким образом, для приведенного механизма получим:

На основе чего можно получить общую формулу для определения передаточного отношения рядового редуктора:

.

Общее передаточное отношение рядового зубчатого механизма постоянно и равно обратному отношению чисел зубьев или радиусов крайних колес. Знак передаточного отношения определяется множителем

, где - число передач внешнего зацепления.

Графическое определение передаточного отношения таких механизмов осуществляется методом планов скоростей (треугольников скоростей). Треугольник скоростей можно построить, если для звена известны линейные скорости не менее двух точек звена (по величине и направлению). Используя этот метод можно получить наглядное представление о характере изменения скоростей от одного вала колеса к другому, а также можно определить графически угловую скорость любого колеса.

,тогда

, где знак отношения определяется по знаку тангенса.

Передаточное отношение рядовых механизмов обычно не велико, так как оно ограничивается предельными размерами крайних колес (1,4), а числа зубьев промежуточных колес (2,3) не влияет на общую величину передаточного отношения. Применяют такие механизмы там, где необходимо изменить вращение ведомого вала, не изменяя при этом направление движения ведущего – коробки передач, либо при передаче движения на значительные расстояния, если нет возможности увеличить размеры ведущего и ведомого колес.

Кинематика ступенчатого зубчатого механизма

Рассмотрим кинематику ступенчатого механизма составленного из трех зубчатых передач: двух внешнего зацепления (1-2) и (3-4) и одной внутреннего зацепления(5-6). Схема механизма изображена на рис.

Аналитическое определение передаточного отношения

Аналитическое определение передаточного отношения основывается на формуле:

Аналитическое определение передаточного отношения.

Заданный планетарный механизм с двумя внешними зацеплениями зубчатых колес. Аналитическое определение передаточного отношения основывается на формуле:

так как колеса 2-3 находятся на одном валу, соответственно вращаются с одинаковой угловой скоростью.

Используя основную теорему Виллиса, для заданного обращенного механизма получим:

По формуле Виллиса

Графическое определение передаточного отношения .

Планетарные механизмы появились на американских автомобилях в начале этого столетия. Их использование на легковых автомобилях и грузовиках малой грузоподъемности было обусловлено неоспоримым преимуществом: минимальные габариты по сравнению с обычными зубчатыми передачами. Вальные коробки передач со скользящими зубчатыми колесами на ранних этапах развития не имели синхронизаторов, и это требовало особой квалификации при переключении передач.

Первые планетарные коробки передач имели только две передачи, хотя имеется информация о том, что в 1906 году Кадиллак использовал планетарный механизм, реализующий три передачи. Ранние конструкции планетарных коробок передач имели ряд существенных недостатков. Они были шумные, имели малую долговечность подшипников (в то время для устанавливки шестерен на валы использовались подшипники скольжения) и из-за перекосов вызванных их неравномерным износом вибрировали при включении ленточных тормозов.

Появление вальных коробок передач с передвижными каретками приводит, в конечном счете, к их большей популярности по сравнению с планетарным коробками, и, практически, к повсеместному их использованию на легковых автомобилях и грузовиках. Однако, на автомобиле Форд-T, планетарная коробка использовалась вплоть до 1928 года.

Планетарные передачи были вновь использованы в 1930 году Bоrg-Warner в автоматической коробке передач "Дженерал Моторс" Hydra-Matic. Проведенный большой объем исследований, а также использование косозубых зацеплений, легированных сталей, термообработки металла и игольчатых подшипников устранили многие недостатки ранних конструкций планетарных передач. Планетарные передачи сегодня имеют широчайший диапазон использования в легковых автомобилях, грузовиках и гусеничной технике.

ОСНОВНЫЕ ПОНЯТИЯ

Определим общие понятия, используемые при рассмотрении зубчатых передач.

Передаточное отношение механизма . Это отношение частоты вращения ведущего вала к частоте вращения ведомого вала.

Понижающая передача . Передача, передаточное отношение которой по абсолютной величине больше 1. В этом случае крутящий момент на ведомом валу механизма больше момента на ведущем валу на величину передаточного отношения, а частота вращения ведомого вала на эту же величину меньше частоты вращения ведущего вала.

Повышающая передача . Передача, передаточное отношение которой по абсолютной величине меньше 1. В этом случае крутящий момент на ведомом валу механизма меньше момента на ведущем валу на величину передаточного отношения, а частота вращения ведомого вала на эту же величину больше частоты вращения ведущего вала.

Прямая передача . Передача, передаточное отношение которой равно 1, т.е. крутящий момент и частота вращения ведомого вала остаются равны частоте вращения и моменту ведущего вала.

УСТРОСТВО И СВОЙСТВА ПЛАНЕТАРНОГО РЯДА (МЕХАНИЗМА)

Конструкции планетарных рядов достаточно разнообразны. Познакомимся с устройством планетарного ряда на примере наиболее простого и часто используемого (рис.1). Он состоит из малого центрального колеса (солнца), которое находится в постоянном зацеплении с шестернями, называемыми сателлитами. Сателлиты могут вращаться относительно осей, установленных в водиле. Зубчатое колесо внутреннего зацепления, называемое большим центральным колесом (эпициклом, короной), находится в постоянном зацеплении с сателлитами и окружает всю конструкцию. Следует отметить, что малое центральное колесо, водило и большое центральное колесо вращаются относительно одной общей оси, в то время, как сателлиты планетарной передачи вращаются относительно собственных осей и вместе с водилом относительно общей оси. При этом следует отметить, что сателлиты планетарной передачи являются составной частью водила.

Название этого механизма происходит от сателлитов, которые подобно планетам, вращаются относительно своих осей и в то же время вокруг малого центрального колеса (солнца).

Что же так привлекает конструкторов к планетарным механизмам? Здесь можно перечислить несколько пунктов:

1 . Все элементы планетарной передачи вращаются относительно общей оси, что делает ее компактной.

2 . Планетарные передачи, не смотря на их компактные размеры, могут передавать большие крутящие моменты по сравнению к другим типами передачи. Это объясняется тем, что момент передается несколькими сателлитами планетарной передачи, что позволяет значительно снизить контактные напряжения на поверхностях зубьев при передаче момента.

3 . Расположение элементов планетарного ряда позволяет относительно легко организовывать их систему управления (имеется в виду оборудование тормозами и блокировочными муфтами).

4 . При удачном выборе кинематической схемы КПД таких передач имеет высокое значение

Основным параметром, определяющим свойства планетарного ряда, является внутреннее передаточное отношение. В общем случае любой планетарный ряд характеризуется шестью внутренними передаточными отношениями. Однако, на практике обычно используется только одно, определяемое как отношение частоты вращения малого центрального к частоте вращения большого центрального колеса при остановленном водиле:

В зависимости от того, как вращаются центральные колеса при остановленном водиле, внутреннее передаточное отношение планетарного ряда может быть либо положительным, либо отрицательным. Если они вращаются в одном и том же направлении, то внутреннее передаточное отношение положительное, в противном случае оно отрицательное. Так для простого планетарного ряда, представленного на рис.1, центральные колеса при остановке водила будут вращаться в различных направлениях, и, следовательно, внутреннее передаточное отношение этого ряда - отрицательное.

Все планетарные ряды в зависимости от знака внутреннего передаточного отношения, определенного при остановленном водиле, классифицируются на два класса:

1. Планетарные ряды с положительным внутренним передаточным отношением.

2. Планетарные ряды с отрицательным внутренним передаточным отношением.

Как уже отмечалось, кинематических схем построения планетарных рядов имеется достаточно большое количество. Наиболее известным планетарным рядом для всех автолюбителей является дифференциал (рис.2), без которого не обходится не один современный автомобиль. Наверное, не многие догадываются, что дифференциал есть не что иное, как планетарный ряд.

Отличительной особенностью дифференциала является то, что он имеет центральные колеса одинакового размера, поэтому внутреннее передаточное отношение этого механизма равно -1. Минус, очевидно, означает, что дифференциал относится ко второму классу планетарных механизмов, т.е. при остановленном водиле центральные колеса вращаются в разные стороны.

Рассмотрим другие типы планетарных рядов. На рисунке 3 представлены планетарные ряды, относящиеся к первому классу.

Примеры построения планетарных рядов, относящихся ко второму классу, представлены на рисунке 4.

Планетарные ряды, изображенные на рисунках 3а, 3в, 4б, 4в, построены с использованием двухвенцовых сателлитов. Планетарный ряд, построенный по схеме 4в, носит название несимметричного дифференциала, а ряд, представленный на рисунке 4г называется планетарным рядом со сцепленными сателлитами.

Как видно из приведенных примеров, планетарный ряд можно построить, используя только внутреннее зацепление (рис.3а), только внешнее зацепление (рис.3в и 4г), только конические передачи (рис.2 и 3в) или с использованием внутреннего и внешнего зацеплений (рис.3б, 4а, 4б).

Уравнение, связывающее угловые скорости () трех основных звеньев любого планетарного ряда (не зависимо от схемы построения) выглядит следующим образом:

Вы спросите: "А как, все-таки, определить величину внутреннего передаточного отношения планетарного ряда i 12 ?". Нет ничего проще. Модуль этой величины можно легко определить, зная число зубьев шестерен, входящих в состав планетарного ряда. Для планетарных рядов с одновенцовыми и сцепленными сателлитами

Для планетарных рядов с двухвенцовыми сателлитами эта величина может быть определена следующим образом:

Таким образом, зная величину внутреннего передаточного отношения, а для конкретного планетарного ряда она постоянна, и имея зависимость, связывающую угловые скорости трех основных звеньев планетарного ряда, можно определить свойства этого механизма.

1. Свойство блокировки планетарного ряда.

Нетрудно показать, что если угловые скорости двух звеньев планетарного ряда равны, то и угловая скорость третьего звена будет равна угловой скорости этих двух звеньев. Пусть, например, 1 =3 , тогда

или

т.е. угловые скорости всех звеньев в этом случае равны, и планетарный ряд будет вращаться как одно целое тело. Аналогичный результат можно получить и в двух других случаях, когда 1 =2 и 2 =3 . Отсюда вытекает известное свойство блокировки планетарного ряда: если установить блокировочную муфту между любыми двумя звеньями планетарного ряда (рис.5), то при ее включении планетарный ряд будет заблокирован, и его передаточное отношение будет равно 1.

2. Свойство работать в редукторном режиме.

Рассмотрим это свойство на примере планетарного ряда второго класса, т.е. с отрицательным внутренним передаточным отношением (i 12 <0). Здесь возможны два варианта.

Первый. 2 =0), водило назначим ведомым звеном планетарного ряда, а малое центральное колесо - ведущим звеном (рис.6а). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью:

т.е. получаем редуктор, передаточное отношение которого на единицу больше внутреннего передаточного отношения самого планетарного ряда.

Второй. Пусть большое центральное колесо будет ведущим звеном планетарного ряда, водило - ведомым звеном, а малое центральное колесо - остановлено, ( =0) (рис.6б). Тогда после небольшого преобразования (1) получим:

т.е. получаем редуктор, передаточное отношение которого близко к единице.

3. Свойство работать в режиме повышающей передачи. Опять-таки, рассмотрим это свойство на примере планетарного ряда второго класса, т.е. с отрицательным внутренним передаточным отношением (i 12 <0) . Здесь также возможны два варианта.

Первый. Пусть большое центральное колесо будет остановлено (2 =0), водило - ведущим звеном планетарного ряда, а малое центральное колесо - ведомым звеном (рис.7а). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью:

Второй. Пусть большое центральное колесо будет ведомым звеном планетарного ряда, водило - ведущим звеном планетарного ряда, а малое центральное колесо - остановлено ( 1 =0) (рис.7б). Тогда в соответствии с (1) передаточное отношение механизма будет определяться следующей зависимостью:

Анализ полученной зависимости показывает, что в этом случае будет получена повышающая передача с передаточным отношением близким к единице.

4. Свойство реверсивности.

Использование этого свойства позволяет организовать передачу заднего хода. Так же, как и в трех предыдущих случаях исследуем возможности реверсивного свойства на примере планетарного ряда второго класса. Здесь возможны, опять-таки два варианта.

Первый. Пусть большое центральное колесо будет ведомым звеном планетарного ряда, водило - остановлено (3 =0), а малое центральное колесо - ведущим звеном (рис.8а). Тогда в соответствии с (1) передаточное отношение механизма будет равно внутреннему передаточному отношению планетарного ряда:

Поскольку для планетарных механизмов второго класса внутреннее передаточное отношение отрицательное, то получаем редуктор с отрицательным передаточным отношением.

Второй. Пусть большое центральное колесо будет ведущим звеном планетарного ряда, водило - остановлено (3 =0), а малое центральное колесо - ведомым звеном (рис.8а). Тогда

Т.е. получаем мультипликатор с отрицательным передаточным отношением (поскольку i 12 <0).

Центральное колесо 1 называется солнечным, а неподвижное 3 - коронным или корончатым. Зубчатое колесо 2 имеющее подвижную ось называется сателлитом. Звено Н называется водилом или поводком. Механизмы, в состав которых входят зубчатые колеса с подвижными осями называются планетарными или дифференциальными.

Планетарными (рис. 14 а) называются механизмы, имеющие одну степень свободы. Дифференциальные (рис. 14 б) механизмы имеют две и более степени свободы.

Эти механизмы обязательно должны быть соосными, то есть оси солнечных колёс должны располагаться на одной и той же прямой линии.

Рассмотрим дифференциальный механизм (рис. 15).

где: n=4; ; .

Таким образом определённость в движении звеньев этого механизма будет в том случае, если будут известны законы движения двух его ведущих звеньев.

Так как сателлиты имеют подвижные оси, то использовать формулы для расчёта передаточного отношения механизмов с неподвижными осями не представляется возможным. В этом случае прибегают к методу инверсии (метод обращённого движения).

Будем рассматривать движение всех колёс относительно водила. Всем звеньям зададим вращательное движение с угловой скоростью водила, но в обратном направлении и найдём скорости всех звеньев механизма. Для этого вычтем угловую скорость водила из всех угловых скоростей колёс.

Таблица 2.

№ Звеньев	Скорость звена в действительном движении (до инверсии)	Скорость звена в обращённом движении (после инверсии)
Колесо 2’

Механизм, полученный в результате инверсии (остановки водила) называется обращённым (рис. 16). В результате получили обычную зубчатую передачу с неподвижными осями.

Эту зависимость (1) называют формулой Виллиса для дифференциальных механизмов.

Если бы было n - колёс, то:

где s – солнечное колесо.

Дифференциальный механизм никакого определённого передаточного отношения не имеет, если ведущим является одно из звеньев (колесо или водило), и приобретает определённость, если ведущих колёс будет два.